I want to get the solution of the equation 
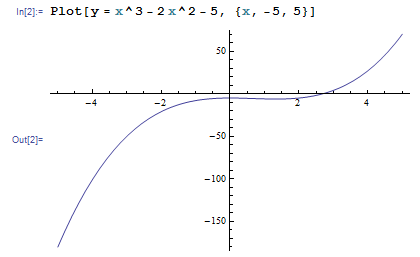
Bisection Method
The first algorithm for the problem is bisection method.
The algorithm bisection method doesn’t require derivation for the equation. It just needs a possible solution range [l, r], then calculates the variable mid as 
, compares the result of func(mid) and zero to adjust solution range, until it finds the target value or go beyond the max number of iterations.
from math import fabs
def func( x ):
return x*x*x - 2*x*x - 5.0
"""
:param y: the target value of functon
:param l: the x-axis value where func(l) < 0
:param r: the x-axis value where func(r) > 0
:param limitErr: the precision
:param maxIterator: max number of iterations
"""
def midfind( y, l, r, limitErr, maxIterator ):
iterator = 1
while iterator <= maxIterator :
mid = ( l + r ) / 2.0
if func( mid ) == 0 or fabs(l-r)/2.0 < limitErr :
return mid, iterator
iterator = iterator + 1
if func(mid) < 0:
l = mid
else:
r = mid
return None, iterator
if __name__ == "__main__":
x, it = midfind( 0, -5, 5, 0.00001, 40 )
print "X is ",x
print "The number of iteractions is ",it
output:
X is 2.69064903259
The number of iteractions is 20
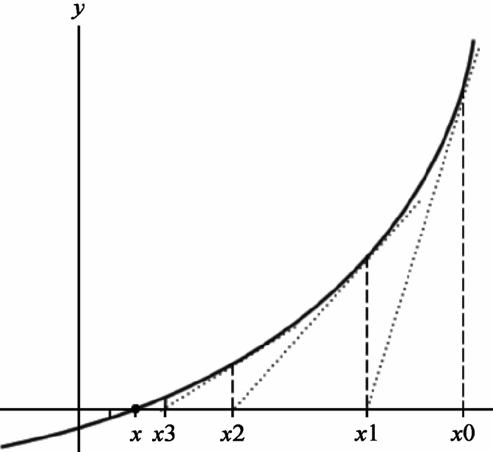
Newton’s Method
We use 
to represent the derivative function of original function 
.
It’s common known that 
.
Then we have 
, its form can be changed to 
.
The equation 
is logical if 
is similar to zero and 
.
So the following equations deduced are the central idea of Newton’s method:
from math import fabs
def func( x ):
return x*x*x - 2*x*x - 5.0
def derivaFunc( x ):
return 3*x*x - 4*x
"""
:param x: the guess value of x where func(x) = 0
:param limitErr: the precision
:param maxIterator: max number of iterations
"""
def newton( x, limitErr, maxIterator ):
iterator = 1
while iterator <= maxIterator :
x1 = x - func(x) / derivaFunc(x)
if fabs(x-x1) < limitErr:
return x1, iterator
else:
x = x1
iterator = iterator + 1
return None, iterator
if __name__ == "__main__":
x, it = newton( 5, 0.00001, 100 )
print "X is ",x
print "The number of iteractions is ",it
output:
X is 2.69064744803
The number of iteractions is 6
Secant Method
The algorithm draws secant lines multiple times until find similar solution.
The secant line intersect with equation curve and get two points of intersection.
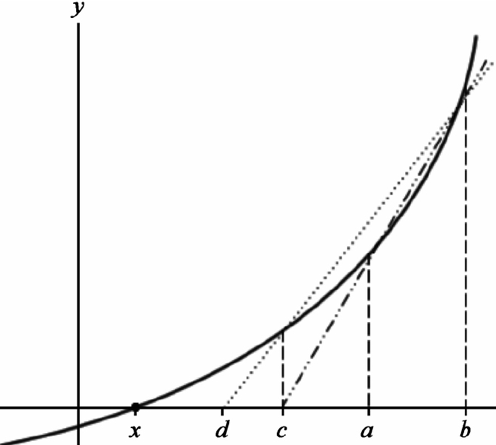
When y is equal to zero, we have the following equation:
Remove y, becase it is equal to 0, we can get:
To get right x value where func(x) = 0, we have to move the secant line from (a,b) to (c, b).
from math import fabs
def func( x ):
return x*x*x - 2*x*x - 5.0
"""
:param a: the x-axis value
:param b: the x-axis value where b > a
:param limitErr: the precision
:param maxIterator: max number of iterations
"""
def secant( a, b, limitErr, maxIterator ):
iterator = 1
while iterator <= maxIterator :
c = b - func(b) * ((b-a)/(func(b)-func(a)))
if fabs(c-b) < limitErr:
return c, iterator
else:
a = b
b = c
iterator = iterator + 1
return None, iterator
if __name__ == "__main__":
x, it = secant( -5, 5, 0.00001, 100 )
print "X is ",x
print "The number of iteractions is ",it
output:
X is 2.69064744803
The number of iteractions is 8
scipy.optimize
The above algorithms are all avaliable in module scipy.optimize, we can import it and use these algorithms directly.
import scipy.optimize as optimize
y = lambda x: x**3.0 - 2*x**2 - 5
dy = lambda x: 3.0*x**2 - 4*x
print "Bisection method: ",optimize.bisect(y, -5, 5, xtol=0.00001)
#The Newton-Raphson method is used if the derivative fprime of func is provided,
#otherwise the secant method is used.
print "Newton method: ",optimize.newton(y, 5, dy, tol=0.00001)
print "Secant method: ",optimize.newton(y, 5, tol=0.00001)
output:
Bisection method: 2.69064903259
Newton method: 2.69064744803
Secant method: 2.69064744805
