Calculate Distance Weight On A Special Vector

Use Transform

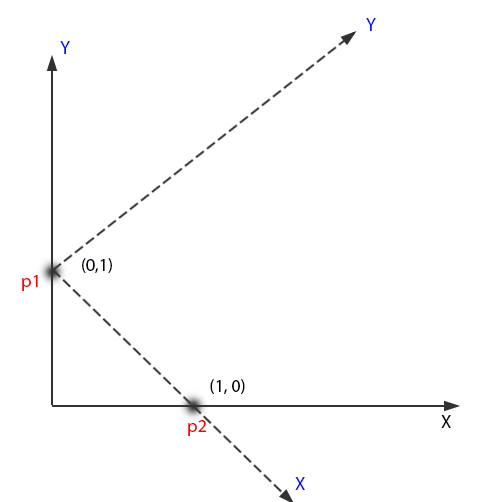
We have both points on the image, the distance weight on the x-axis between the two points is 1. What is the distance weight on the vector (p1−p2) between the two points?
It’s easy to calculate the result because we know Pythagorean theorem and the special direction is exactly p2−p1. But I write an another way to get the value here.
We can rotate the X axis to go through p1 and p2. Then the result of Xp2​−Xp1​ is the answer.

Code snippet:

using namespace std;

int main()
{
    PointStruct p1( 0, 1, 0 );
    PointStruct p2( 1, 0, 0 );
    vtkSmartPointer<vtkTransform> transform =
            vtkSmartPointer<vtkTransform>::New();

    PointStruct v1( 1, 0, 0 );
    PointStruct v2 = p2 - p1;
    PointStruct rotateAxis = v1^v2;
    //double angle = acos( v1.Dot( v2 ) ) * 180.0 / vtkMath::Pi();
    double angle = vtkMath::AngleBetweenVectors( v1.point, v2.point );
    angle = vtkMath::DegreesFromRadians( angle );
    printf( "angle: %lf\n", angle );
    transform->RotateWXYZ( -angle, rotateAxis.point );
    transform->Update();
    transform->InternalTransformPoint( p1.point, p1.point );
    transform->InternalTransformPoint( p2.point, p2.point );
    printf( "p1: (%lf, %lf, %lf)\n", p1[0], p1[1], p1[2] );
    printf( "p2: (%lf, %lf, %lf)\n", p2[0], p2[1], p2[2] );
    double result = p2[0] - p1[0];
    PointStruct tmp = p2 - p1;
    printf( "result: %lf\n", result );
    return 0;
}

Output:

angle: 45.000000
p1: (-0.707107, 0.707107, 0.000000)
p2: (0.707107, 0.707107, 0.000000)
result: 1.414214

Create Plane

We can also create a plane which take p1 as origin and take the special vector as its normal.
Then the distance weight on the normal vector between p1 and p2 is the distance between p2 and plane.

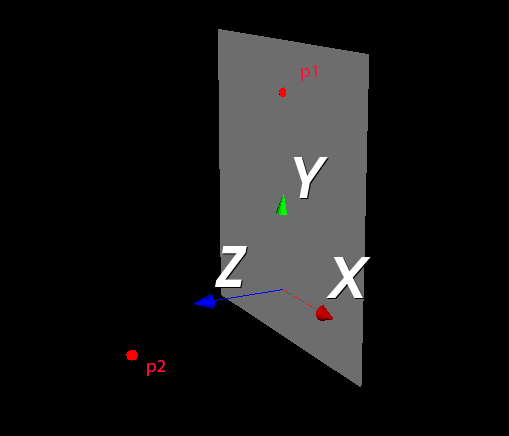
Interfaces:

vtkPlane::ProjectPoint
vtkMath::Distance2BetweenPoints