Why Concatenate User Transform When Scale Object

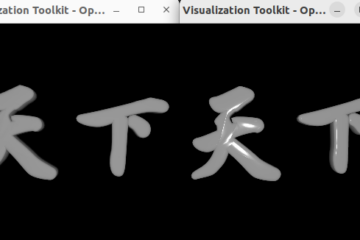
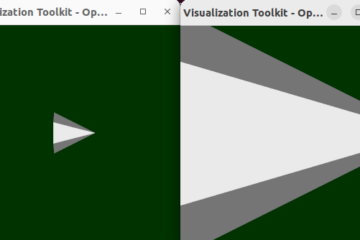
I write the reason why concatenate transform and its inversed transform for offTrans in scale operation based on the article Rotate, Translate And Scale For Camera

    vtkSPtrNew( scaleTrans, vtkTransform );
    scaleTrans->Scale( factor, factor, 1 );
    scaleTrans->Update();

    vtkSPtrNew( offTrans, vtkTransform );
    offTrans->Concatenate( worldTrans );
    offTrans->Concatenate( scaleTrans );
    offTrans->Concatenate( worldInversedTrans );
    offTrans->Update();
    PointStruct line( 1, 0, 0 );
    offTrans->TransformVector( line.point, line.point );
    cout << "line: " << line;

We got the following result when zooming in or zoom out after rotating the image.

line: PointStruct [0.847532, -5.80018e-05, 0.0566997]
line: PointStruct [0.847532, -5.80018e-05, 0.0566997]
line: PointStruct [1.18449, 7.01822e-05, -0.0686066]
line: PointStruct [1.18449, 7.01822e-05, -0.0686066]
line: PointStruct [0.847532, -5.80018e-05, 0.0566997]

If we set offTrans in the way:

    vtkSPtrNew( offTrans, vtkTransform );
    offTrans->Concatenate( scaleTrans );
    offTrans->Update();

The result showed that it just enlarge the image on the x-axes direction, but we had rotated the image so it will bring disaster.

line: PointStruct [0.826446, 0, 0]
line: PointStruct [0.826446, 0, 0]
line: PointStruct [1.21, 0, 0]
line: PointStruct [1.21, 0, 0]
line: PointStruct [1.21, 0, 0]

For offTrans,
reduce image: (dynamic matrix, elements in the matrix will change as rotating image)

enlarge image: (dynamic matrix)

For single scale transform,
reduce image: (static matrix)

enlarge image: (static matrix)

There are two important common senses for matrix (except a few special situations).

The second inequality is the reason why we need to concatenate image user transform and its inversed transform.

cout << "=========== matrix =========\n";
scaleTrans->PrintSelf( std::cout, vtkIndent() );

vtkSPtrNew( offTrans, vtkTransform );
offTrans->Concatenate( worldTrans );
offTrans->Concatenate( scaleTrans );
offTrans->PrintSelf( std::cout, vtkIndent() );

offTrans->Concatenate( worldInversedTrans );
offTrans->Update();
offTrans->PrintSelf( std::cout, vtkIndent() );
cout << "=========== end =========\n";

Matrix output:

//Original matrix
0.826446 0 0 0 
0 0.826446 0 0 
0 0 1 0 
0 0 0 1 

335.405 0.382796 0.322301 0 
-2.66527 354.24 0.0187427 0 
-114.165 -7.14541 0.946452 0 
0 0 0 1 

//new result matrix
0.844475 0.0010484 0.0529412 0 
0.0010484 0.826507 0.00307868 0 
0.0529412 0.00307868 0.981911 0 
0 0 0 1