Use Dot Product And Cross Product To Compute The Distance From A Point To Line

The article introduces two ways to calculate the distance from a point to a line. One use dot product by two vectors to get distance vector, and the other use cross product by vectors to achieve it.

Let’s assume the point is P, two endpoints of the line are L1 and L2.

Dot Product

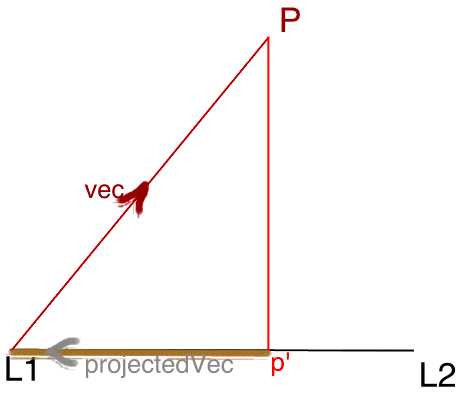
The distance vector is (p’p) as the above image.

using namespace std;

int main()
{
    PointStruct l1( 0, 0, 0 );
    PointStruct l2( 3, 0, 0 );
    PointStruct p( 2, 3, 0 );
    PointStruct line = l1 - l2;
    line.Unit();
    PointStruct vec = p - l1;

    double dotValue = vec.Dot( line );
    PointStruct projectedVec = line*dotValue;
    PointStruct final = -projectedVec + vec;

    std::cout << final.Length() << std::endl;
    return 0;
}

Output:

3

Cross Product

The cross product of two vectors is a new vector that is orthogonal to them. But it can also indicate the distance from a point to line.

int main()
{
    PointStruct l1( 0, 0, 0 );
    PointStruct l2( 3, 0, 0 );
    PointStruct p( 2, 3, 0 );
    PointStruct line = l1 - l2;
    line.Unit();
    PointStruct vec = p - l1;

    PointStruct final = line ^ vec;
    printf( "final: (%lf, %lf, %lf)\n", final[0], final[1], final[2] );
    std::cout << final.Length() << std::endl;
    return 0;
}

Output:

final: (0.000000, 0.000000, -3.000000)
3