VTK – Local Coordinate System

We want to know the world coordinate of a point on a 3D widget event though we don’t know the widget’s position on the world coordinate system. I get a matrix from an actor and create a temporal vtkTransform object, then the function TransformDoublePoint can give me the real coordinate value of a single point on the 3D model. This is my solution for calculating real coordinate. It’s possible to get an inverse transform if we know coordinates of a point, the direction of the X-axis and the direction of the Y-axis of the 3D model. That means we have a second way to calculate the point’s position. For example, we have point (p0, p1, p2), vector (x0, x1, x2) and vector (y0, y1, y2). The third vector (z0, z1, z2) is the cross product result of vector1 and vector2.

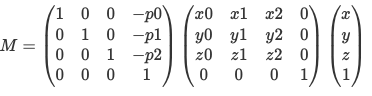
For vtkTransform::Concatenate: In homogeneous matrix notation, M = M*A where M is the current transformation matrix and A is the applied matrix. The default is PreMultiply.

The local matrix can give us information about the coordinate system transform. Let’s read an example.

Before rotating plane:

#include <iostream>
#include <vtkSmartPointer.h>
#include <vtkSphereSource.h>
#include <vtkActor.h>
#include <vtkConeSource.h>
#include <vtkRenderer.h>
#include <vtkRenderWindow.h>
#include <vtkPolyDataMapper.h>
#include <vtkProperty.h>
#include <vtkRenderWindowInteractor.h>
#include <vtkLight.h>
#include <vtkCamera.h>
#include <vtkActor2D.h>
#include <vtkTransform.h>
#include <vtkLinearTransform.h>
#include <vtkPlaneSource.h>

#include "tool.h"

using namespace std;

#define vtkSPtr vtkSmartPointer
#define vtkSPtrNew(Var, Type) vtkSPtr<Type> Var = vtkSPtr<Type>::New();

vtkSmartPointer<vtkTransform> CreateLocalTrans(PointStruct origin, PointStruct xDir, PointStruct yDir)
{
    vtkSPtrNew( resultTrans, vtkTransform );
    PointStruct zDir = xDir ^ yDir;
    zDir.Unit();

    double elements1[16] = { xDir[0], xDir[1], xDir[2], 0,
                            yDir[0], yDir[1], yDir[2], 0,
                            zDir[0], zDir[1], zDir[2], 0,
                            0, 0, 0, 1 };

    resultTrans->Concatenate(elements1);     //rotation

    double elements2[16] = { 1, 0, 0, -origin[0],
                             0, 1, 0, -origin[1],
                             0, 0, 1, -origin[2],
                             0, 0, 0, 1 };

    resultTrans->Concatenate(elements2);    //translation
    resultTrans->Update();

    return resultTrans;
}

int main()
{
    setbuf( stdout, nullptr );

    // ============ plane start ================
    vtkSmartPointer<vtkPlaneSource> planeSource =
            vtkSmartPointer<vtkPlaneSource>::New();
    planeSource->SetOrigin( 0, 0, 0 ); //Relative
    planeSource->SetPoint1( 0, 2, 0 );
    planeSource->SetPoint2( 2, 0, 0 );

    vtkSmartPointer<vtkPolyDataMapper> planeMapper =
            vtkSmartPointer<vtkPolyDataMapper>::New();
    planeMapper->SetInputConnection( planeSource->GetOutputPort() );

    vtkSmartPointer<vtkActor> planeActor =
            vtkSmartPointer<vtkActor>::New();
    planeActor->SetMapper( planeMapper );
    //planeActor->SetPosition( 1, 1, 0 );
    // ============ plane end ================

    // ============ sphere start ================
    vtkSmartPointer<vtkSphereSource> sphereSource =
            vtkSmartPointer<vtkSphereSource>::New();
    sphereSource->SetCenter( 2, 2, 0 );
    sphereSource->SetRadius( 0.1 );

    vtkSmartPointer<vtkPolyDataMapper> sphereMapper =
            vtkSmartPointer<vtkPolyDataMapper>::New();
    sphereMapper->SetInputConnection( sphereSource->GetOutputPort() );

    vtkSmartPointer<vtkActor> sphereActor =
            vtkSmartPointer<vtkActor>::New();
    sphereActor->SetMapper( sphereMapper );
    sphereActor->GetProperty()->SetColor( 1, 0, 0 );
    // ============ plane end ================

    // Change actor status.
    planeActor->RotateY( 90 );

    // The first way
    vtkSmartPointer<vtkTransform> transform = vtkSmartPointer<vtkTransform>::New();
    transform->SetMatrix( planeActor->GetMatrix() );
    double pt1[3] = { 2, 2, 0 };
    double pt2[3] = { 1, 0, 0 };
    double *pt3 = transform->TransformDoublePoint( pt1 );
    printf( "(%lf, %lf, %lf)\n", pt3[0], pt3[1], pt3[2] );
    // (0.000000, 2.000000, -2.000000)

    // The second way
    PointStruct HomePt( 0, 0, 0 );
    PointStruct xPt( 0, 0, -1 );
    PointStruct yPt( 0, 1, 0 );
    vtkSmartPointer<vtkTransform> localTransform = CreateLocalTransform( HomePt, xPt, yPt );
    localTransform->Inverse();  // inverse get matrix's transform
    pt3 = localTransform->TransformDoublePoint( pt2 );
    printf( "(%lf, %lf, %lf)\n", pt3[0], pt3[1], pt3[2] );

    // localTransform
    // x: (0.000000, 0.000000, 1.000000)
    // y: (0.000000, 1.000000, 0.000000)
    // z: (-1.000000, 0.000000, 0.000000)

    // localTransform Inverse
    // x: (0.000000, 0.000000, -1.000000)
    // y: (0.000000, 1.000000, 0.000000)
    // z: (1.000000, 0.000000, 0.000000)

    vtkSmartPointer<vtkRenderer> renderer =
            vtkSmartPointer<vtkRenderer>::New();
    renderer->AddActor( planeActor );
    renderer->AddActor( sphereActor );
    renderer->SetBackground( 0, 0, 0 );

    vtkSmartPointer<vtkRenderWindow> renderWindow =
            vtkSmartPointer<vtkRenderWindow>::New();
    renderWindow->AddRenderer( renderer );

    vtkSmartPointer<vtkRenderWindowInteractor> renderWindowInteractor =
            vtkSmartPointer<vtkRenderWindowInteractor>::New();
    renderWindowInteractor->SetRenderWindow( renderWindow );

    renderer->ResetCamera();
    renderWindow->Render();
    renderWindowInteractor->Start();
    return 0;
}

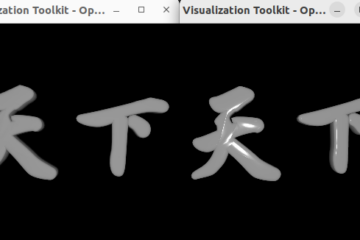
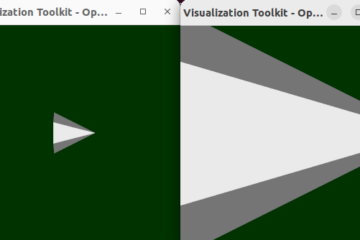
After rotating plane: