We had found the closest line between points in the 2D world by least squares, link: Find Closest Line Between Points In 2D By Least Squares
I will show how to find the closest plane closest to a few random points in the 3D environment.
We know that the sum of square distances from point to plane can be calculated.
![]()
Similar to our last example, Find Closest Line Between Points In 2D By Least Squares, If the derivatives of ![]() to variables, respectively become zero, the minimum value will occur.
to variables, respectively become zero, the minimum value will occur.
We have:
![]()
![]()
![]()
We know:
![]()
![]()
So we get:
![]()
![]()
![]()
![]()
![]()
![]()
we can’t find a simple linear matrix to represent ![]() . So it’s impossible to get results by matrix directly. Levenberg-Marquardt is a popular alternative to find the minimum sum of squares of nonlinear functions. It improves the Gauss-Newton method for the nonlinear-least squares optimization problem.
. So it’s impossible to get results by matrix directly. Levenberg-Marquardt is a popular alternative to find the minimum sum of squares of nonlinear functions. It improves the Gauss-Newton method for the nonlinear-least squares optimization problem.
Find the implementation of the algorithm in GitHub, levmar-2.6.
The following demo show how to use it and draw points and the closest plane by VTK.
cmake_minimum_required(VERSION 3.16)
project(explore3D)
set(CMAKE_CXX_STANDARD 14)
find_package( VTK REQUIRED )
include( ${VTK_USE_FILE} )
set( LEVMAR_PATH /Users/weiyang/Downloads/levmar-2.6 )
include_directories( ${LEVMAR_PATH} )
set( header_files
"../point.hpp" )
set( src_files
${LEVMAR_PATH}/Axb.c
${LEVMAR_PATH}/lm.c
${LEVMAR_PATH}/lmbc.c
${LEVMAR_PATH}/lmblec.c
${LEVMAR_PATH}/lmbleic.c
${LEVMAR_PATH}/lmlec.c
${LEVMAR_PATH}/misc.c
)
add_executable(explore3D main.cpp ${header_files} ${src_files} )
target_link_libraries( ${PROJECT_NAME} ${VTK_LIBRARIES} )
main.cpp:
#include <iostream>
#include <levmar.h>
#include <vector>
#include <iostream>
#include <vtkPolyData.h>
#include <vtkProperty.h>
#include <vtkPolyDataMapper.h>
#include <vtkActor.h>
#include <vtkPlane.h>
#include <vtkRenderer.h>
#include <vtkRenderWindow.h>
#include <vtkRenderWindowInteractor.h>
#include <vtkPoints.h>
#include "../point.hpp"
#include <vtkPlane.h>
#include <vtkPlaneSource.h>
#include <vtkTransform.h>
#define vtkSPtr vtkSmartPointer
#define vtkSPtrNew(Var, Type) vtkSPtr<Type> Var = vtkSPtr<Type>::New();
void Dis2FromPtToPlane( double *planeParas, double *dis2, int m, int n, void *data );
void DerivativeOfDis2(double *planeParas, double *derivative, int m, int n, void *data);
int main() {
std::vector<Point> samplePts{ {-25.1339, -5.76816, -0.995864},
{-14.7021, -2.73063, 18.1714},
{-0.458432, -1.09882, 24.679},
{12.8826, -1.73559, 17.6288},
{23.2548, -4.19458, -1.25975},
{23.2548, -2.19458, 6.25975} };
double data[samplePts.size()*3];
Point center( 0, 0,0 );
for( int i = 0; i < samplePts.size(); ++i )
{
data[i*3] = samplePts[i][0];
data[i*3+1] = samplePts[i][1];
data[i*3+2] = samplePts[i][2];
center = center + samplePts[i];
}
center /= samplePts.size();
double paras[6] = { 1, 1, 1, center[0], center[1], center[2] };
double *target = new double[ samplePts.size() ];
for( int i = 0; i < samplePts.size(); ++i )
{
target[i] = 0;
}
// m: parameters count; n: points count
double iterateMax = 1000;
double opts[LM_OPTS_SZ], info[LM_INFO_SZ];
opts[0] = LM_INIT_MU;
opts[1] = opts[2] = 1E-15;
opts[3] = 1E-20;
opts[4]= LM_DIFF_DELTA;
dlevmar_der( Dis2FromPtToPlane, DerivativeOfDis2, paras, target, 6, samplePts.size(), iterateMax,
opts, info, nullptr, nullptr, data );
delete [] target;
// =============== draw plane ==============
vtkSPtrNew( plane, vtkPlane );
plane->SetNormal( paras[0], paras[1], paras[2] );
plane->SetOrigin( paras[3], paras[4], paras[5] );
vtkSmartPointer<vtkPlaneSource> planeSource =
vtkSmartPointer<vtkPlaneSource>::New();
planeSource->SetCenter( plane->GetOrigin() );
planeSource->SetNormal( plane->GetNormal() );
planeSource->Update();
vtkSmartPointer<vtkPolyDataMapper> planeMapper =
vtkSmartPointer<vtkPolyDataMapper>::New();
planeMapper->SetInputData( planeSource->GetOutput() );
planeMapper->Update();
int scaleValue = 60;
vtkSmartPointer<vtkActor> planeActor =
vtkSmartPointer<vtkActor>::New();
planeActor->SetMapper( planeMapper );
planeActor->GetProperty()->SetColor( 0, 1, 1 );
planeActor->GetProperty()->SetOpacity( 0.5 );
Point originPt( plane->GetOrigin() );
vtkSPtrNew( trans, vtkTransform );
trans->Translate( originPt.point );
trans->Scale( scaleValue, scaleValue, scaleValue );
trans->Translate( (-originPt).point );
planeActor->SetUserTransform( trans );
// =============== draw points =============
vtkSPtrNew( polyData, vtkPolyData );
vtkSPtrNew( points, vtkPoints );
vtkSPtrNew( cells, vtkCellArray );
for( int i = 0; i < samplePts.size(); ++i )
{
points->InsertNextPoint( samplePts[i].point );
vtkIdType ids[] = { i };
cells->InsertNextCell( 1, ids );
}
polyData->SetPoints( points );
polyData->SetVerts( cells );
polyData->Modified();
vtkSPtrNew( mapper, vtkPolyDataMapper );
mapper->SetInputData( polyData );
vtkSPtrNew( actor, vtkActor );
actor->SetMapper( mapper );
actor->GetProperty()->SetPointSize( 5 );
vtkSPtrNew( renderer, vtkRenderer );
renderer->AddActor( actor );
renderer->AddActor( planeActor );
renderer->SetBackground( 0, 0, 0 );
vtkSPtrNew( renderWindow, vtkRenderWindow );
renderWindow->AddRenderer( renderer );
vtkSPtrNew( renderWindowInteractor, vtkRenderWindowInteractor );
renderWindowInteractor->SetRenderWindow( renderWindow );
renderer->ResetCamera();
renderWindow->Render();
renderWindowInteractor->Start();
return 0;
}
void Dis2FromPtToPlane( double *planeParas, double *dis2, int m, int n, void *data )
{
double *inData = (double *)data;
double M = planeParas[0]*planeParas[0] + planeParas[1]*planeParas[1] + planeParas[2]*planeParas[2];
for( int i = 0; i < n; ++i )
{
double N0 = (inData[i*3] - planeParas[3])*planeParas[0] +
(inData[i*3+1] - planeParas[4])*planeParas[1] +
(inData[i*3+2] - planeParas[5])*planeParas[2];
double N = N0*N0;
dis2[i] = N/M;
}
}
void DerivativeOfDis2(double *planeParas, double *derivative, int m, int n, void *data)
{
double *inData = (double *)data;
double M = planeParas[0]*planeParas[0] + planeParas[1]*planeParas[1] + planeParas[2]*planeParas[2];
for( int i = 0; i < n; ++i ) {
double N0 = (inData[i * 3] - planeParas[3]) * planeParas[0] +
(inData[i * 3 + 1] - planeParas[4]) * planeParas[1] +
(inData[i * 3 + 2] - planeParas[5]) * planeParas[2];
double N = N0*N0;
//dA
derivative[i*6] = 2*N0*(inData[i*3] - planeParas[3])*M - 2*planeParas[0]*N;
derivative[i*6] /= (M*M);
//dB
derivative[i*6+1] = 2*N0*(inData[i*3+1] - planeParas[4])*M - 2*planeParas[1]*N;
derivative[i*6+1] /= (M*M);
//dC
derivative[i*6+2] = 2*N0*(inData[i*3+2] - planeParas[5])*M - 2*planeParas[2]*N;
derivative[i*6+2] /= (M*M);
//dx0
derivative[i*6+3] = 2*N0*(-planeParas[0]) / M;
//dy0
derivative[i*6+4] = 2*N0*(-planeParas[1]) / M;
//dz0
derivative[i*6+5] = 2*N0*(-planeParas[2]) / M;
}
}
Result:


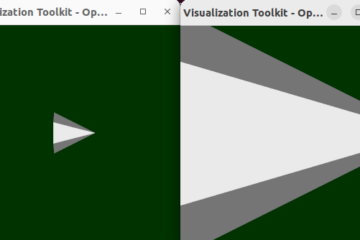
[…] post is similar to Find Closest Plane Between Points In 3D By Levmar Algorithm. The vtkPlane in vtk9.0.2 or the newer version provides a way to calculate the fitting plane for a […]