CGAL: Area of Parallelogram And Volume Of Triple Vectors

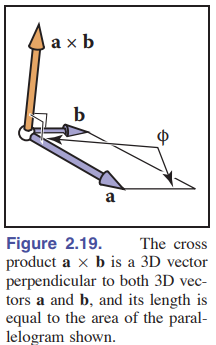
Area of Parallelogram

We can get the third vector by cross product of two vectors, the new vector is perpendicular to the first vectors.
The length of the third vector is equal to the area of the parallelogram formed by and . But it’s a signed result for area.

#include <CGAL/Exact_predicates_exact_constructions_kernel.h>
#include <CGAL/number_utils.h>
#include <iostream>
#include <cmath>

using namespace std;

typedef CGAL::Exact_predicates_exact_constructions_kernel K;
typedef K::Point_3 Point;
typedef K::Vector_3 Vector;

int main()
{
    CGAL::set_mode( cout, CGAL::IO::PRETTY );
    Vector U( Point(0, 0, 0 ), Point(2, 0, 0) );
    Vector V( Point(0, 0, 0 ), Point(3, 2, 0) );
    Vector W = CGAL::cross_product( U, V );
    auto tmp = W.squared_length(); // cpp11::result_of<typename R::Compute_square...>
    auto value = tmp.exact().get_d();
    double result = CGAL::sqrt( value );
    cout << result << endl;
    return 0;
}

Output:

4

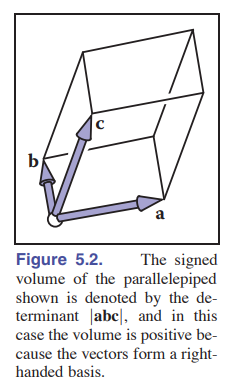
Volume Of Triple Vectors

The volume of the vectors , , and can be calculated by determinant.

We need to use dot product and cross product in the process.

#include <CGAL/Exact_predicates_exact_constructions_kernel.h>
#include <CGAL/number_utils.h>
#include <iostream>
#include <cmath>

using namespace std;

typedef CGAL::Exact_predicates_exact_constructions_kernel K;
typedef K::Point_3 Point;
typedef K::Vector_3 Vector;

int main()
{
    CGAL::set_mode( cout, CGAL::IO::PRETTY );
    Vector U( Point(0, 0, 0 ), Point(2, 2, 0) );
    Vector V( Point(0, 0, 0 ), Point(4, 0, 0) );
    Vector W( Point(0, 0, 0 ), Point(2, 2, 4) );
    auto tmp = CGAL::cross_product( U, V ) * W;

    tmp = CGAL::abs( tmp.exact() );
    cout << tmp << endl;
    return 0;
}

Output:

32

We also know the geometry meaning of the determinant, it’s sign volumn value for three vectors.

So we can calculate the area by determinant.

    auto tmp = CGAL::determinant( U, V, W );
    tmp = CGAL::abs( tmp.exact() );
    cout << tmp << endl;