Compare Cardinal Spline and Uniform Cubic Spline

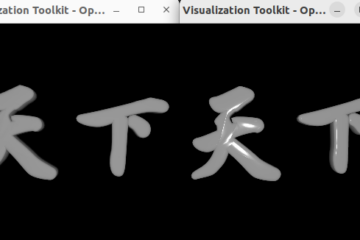
Uniform Cubic Spline To Smooth Segments

Change input points and use the Cubic piecewise function introduced in Basic functions for B-Spline to create smooth curve.

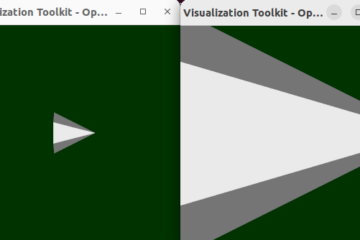
The left renderer shows polygon lines through original points, and the right one is the smooth curve generated by algorithm.

std::vector<Point> originalPts = { Point(2, 0, 0), Point(0, 2, 0), Point(2, 4, 0), Point(4, 2, 0), Point(6, 4, 0), Point(8, 2, 0), Point(6, 0, 0) };

//...

int main(int argc, char* argv[])
{
    double elements[16] = { -1, 3, -3, 1,
                          3, -6, 0, 4,
                          -3, 3, 3, 1,
                          1, 0, 0, 0};
    vtkSmartPointer<vtkTransform> trans = vtkSmartPointer<vtkTransform>::New();
    trans->SetMatrix( elements );

    std::vector<Point> input2Pts;
    auto getVarInVec = [](std::vector<Point> __originalPts, int index){
        if(index >= __originalPts.size())
        {
            return __originalPts[__originalPts.size()-1]; //Point(0, 0, 0);
        }
        if(index < 0)
        {
            return __originalPts[0];
        }
        return __originalPts[index];
    };
    for( int i = -1; i < 5; ++i )
    {
        for(double u = 0; u < 1; u=u+0.1)
        {
            double vec[4] = { u*u*u, u*u, u, 1 };
            double newVec[4];
            trans->MultiplyPoint(vec, newVec);
            Point newPt = (getVarInVec(originalPts, i+0)*newVec[0]+getVarInVec(originalPts, i+1)*newVec[1]+getVarInVec(originalPts, i+2)*newVec[2]+getVarInVec(originalPts, i+3)*newVec[3])*1/6.0;
            input2Pts.push_back( newPt );
        }
    }

//...

Cardinal Spline To Smooth Segments

A Cardinal Spline is typically defined by a set of control points or key points through which the curve passes. These control points, along with tangent vectors at each point, determine the shape of the spline. The tangent vectors at the control points indicate the direction and magnitude of the curve’s curvature at those points.

The mathematical formula for a Cardinal Spline is often expressed as a piecewise cubic function:

Here, S(t) represents the position on the spline at parameter t, P1 and P2 are the positions of the two neighboring control points, and T1 and T2 are the tangent vectors at those control points.

The tangent vectors T1 and T2 in a Cardinal Spline are computed based on the positions of the neighboring control points P1 and P2. To calculate T1 and T2, you can use the following formulas:

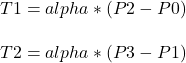
The parameter alpha is a tension parameter that controls the tightness or looseness of the curve. You can adjust the value of alpha to influence the shape of the Cardinal Spline. Typically, alpha is in the range of -1 to 1.

The parameter “t” in the description of the Cardinal Spline is typically a value that varies from 0 to 1, and it’s used to interpolate along the curve. You can calculate the position on the Cardinal Spline by varying the parameter “t” within this range.

#include <vtkActor.h>
#include <vtkCleanPolyData.h>
#include <vtkDistancePolyDataFilter.h>
#include <vtkNamedColors.h>
#include <vtkNew.h>
#include <vtkPointData.h>
#include <vtkPolyDataMapper.h>
#include <vtkPolyDataReader.h>
#include <vtkProperty.h>
#include <vtkRenderWindow.h>
#include <vtkRenderWindowInteractor.h>
#include <vtkRenderer.h>
#include <vtkScalarBarActor.h>
#include <vtkSmartPointer.h>
#include <vtkSphereSource.h>
#include <vtkSTLReader.h>
#include <vtkTransform.h>
#include <vtkMatrix4x4.h>


#include <vector>
#include <list>
#include "point.hpp"


#define vtkSPtr vtkSmartPointer
#define vtkSPtrNew(Var, Type) vtkSPtr<Type> Var = vtkSPtr<Type>::New();


std::vector<Point> originalPts = { Point(2, 0, 0), Point(0, 2, 0), Point(2, 4, 0), Point(4, 2, 0), Point(6, 4, 0), Point(8, 2, 0), Point(6, 0, 0) };


vtkSmartPointer<vtkPolyData> ShowListByLine(std::vector<Point> list)
{
    vtkSPtrNew( result, vtkPolyData );
    vtkSPtrNew( resultPts, vtkPoints );
    vtkSPtrNew( resultLines, vtkCellArray );
    for( int i = 0; i < list.size(); ++i )
    {
        resultPts->InsertNextPoint( list[i].point );
    }
    for( int i = 0; i < list.size()-1; ++i )
    {
        vtkIdType pts[2] = { i, i + 1 };
        resultLines->InsertNextCell( 2, pts );
    }
    result->SetPoints( resultPts );
    result->SetLines( resultLines );
    result->Modified();
    return result;
}


int main(int argc, char* argv[])
{
    std::vector<Point> input2Pts;
    auto getVarInVec = [](std::vector<Point> __originalPts, int index){
        if(index >= __originalPts.size())
        {
            return __originalPts[__originalPts.size()-1]; //Point(0, 0, 0);
        }
        if(index < 0)
        {
            return __originalPts[0];
        }
        return __originalPts[index];
    };
    double alpha = 0.5;
    for( int i = 0; i < 6; ++i )
    {
        Point Ti1 = alpha * (originalPts[i+1] - originalPts[i-1]);
        Point Ti2 = alpha * (originalPts[i+2] - originalPts[i]);
        for(double u = 0; u < 1; u=u+0.1)
        {
            double vec1[4] = { 2*u*u*u - 3*u*u + 1, u*u*u - 2*u*u + u, -2*u*u*u + 3*u*u, u*u*u-u*u };
            Point vec2[4] = { getVarInVec(originalPts, i), Ti1, getVarInVec(originalPts, i+1), Ti2 };
            Point newPt = vec1[0]*vec2[0] + vec1[1]*vec2[1] + vec1[2]*vec2[2] + vec1[3]*vec2[3];
            input2Pts.push_back( newPt );
        }
    }

    vtkSmartPointer<vtkPolyData> input1 = ShowListByLine( originalPts );
    vtkSmartPointer<vtkPolyData> input2 = ShowListByLine( input2Pts );
    vtkNew<vtkRenderWindow> renWin;
    renWin->SetSize(1200, 500);

    vtkNew<vtkRenderWindowInteractor> renWinInteractor;
    renWinInteractor->SetRenderWindow(renWin);

    double leftViewport[4] = {0.0, 0.0, 0.5, 1.0};
    double rightViewport[4] = {0.5, 0.0, 1.0, 1.0};

    vtkSPtrNew( mapper1, vtkPolyDataMapper );
    mapper1->SetInputData( input1 );
    vtkSPtrNew( actor1, vtkActor );
    actor1->SetMapper( mapper1 );

    vtkSPtrNew( mapper2, vtkPolyDataMapper );
    mapper2->SetInputData( input2 );
    vtkSPtrNew( actor2, vtkActor );
    actor2->SetMapper( mapper2 );

    // Setup renderers
    vtkSPtrNew( leftRenderer, vtkRenderer );
    leftRenderer->SetViewport( leftViewport );
    leftRenderer->AddActor( actor1 );
    leftRenderer->SetBackground(.6, .5, .4);
    leftRenderer->ResetCamera();

    vtkSPtrNew( rightRenderer, vtkRenderer );
    rightRenderer->SetViewport(rightViewport);
    rightRenderer->AddActor( actor2 );
    rightRenderer->SetBackground(.4, .5, .6);
    rightRenderer->SetActiveCamera( leftRenderer->GetActiveCamera() );

    renWin->AddRenderer( leftRenderer );
    renWin->AddRenderer( rightRenderer );

    renWin->Render();
    renWinInteractor->Start();

    return EXIT_SUCCESS;
}

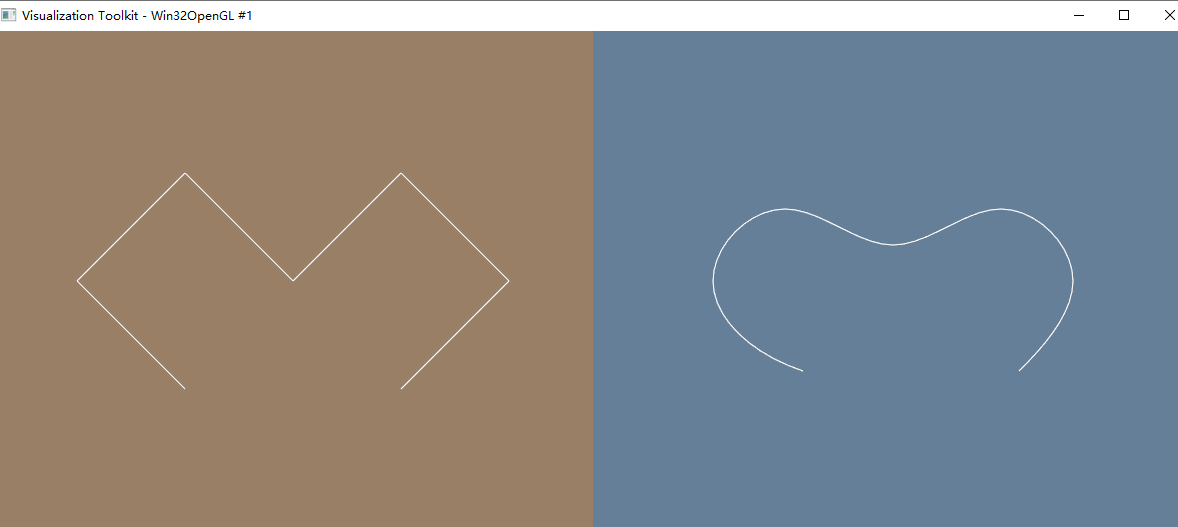
Result:

The choice of alpha will affect the curvature and tightness of the curve. A positive value of alpha will produce a more rounded curve, while a negative value will create a more pointed or angular curve.
For example,

double alpha = -0.5;

Result: