Cross Product
Let’s define vector ![]() and
and ![]() and their cross product
and their cross product ![]() .
.
As known that ![]() , so we have:
, so we have:
![Rendered by QuickLaTeX.com \[\vec{w} = \vec{u} \times \vec{v} = \begin{pmatrix} u_1 & u_2 & u_3 \end{pmatrix} \begin{pmatrix} 0 & -v_3 & v_2 \\ v_3 & 0 & -v_1 \\ -v_2 & v_1 & 0 \end{pmatrix}\]](https://www.weiy.city/wp-content/ql-cache/quicklatex.com-b227998eee6d89ea145d49acfed19306_l3.png)
The cross product is antisymmetric due to its definition.
![]()
Dot Product
![]()
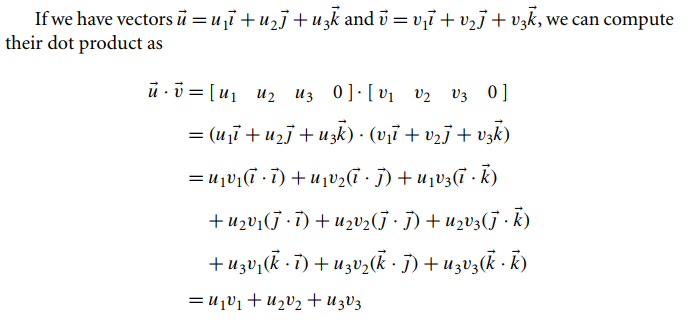
So we can write the dot product of two vectors as the matrix form.
![Rendered by QuickLaTeX.com \[\vec{u} \cdot \vec{v} = \begin{pmatrix} u_1 & u_2 & u_3 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix}\]](https://www.weiy.city/wp-content/ql-cache/quicklatex.com-fd74da97540550ed5d4855949ed93ed4_l3.png)
Tensor Product
If we have the vector T:
![]()
We can write it by matrix based on the previous knowledges.
![Rendered by QuickLaTeX.com \[\vec{t} = \begin{pmatrix} u_1 & u_2 & u_3 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix} \begin{pmatrix} w_1 & w_2 & w_3 \end{pmatrix} = \begin{pmatrix} u_1 & u_2 & u_3 \end{pmatrix} \begin{pmatrix} v_1w_1 & v_1w_2 & v_1w_3 \\ v_2w_1 & v_2w_2 & v_2w_3 \\ v_3w_1 & v_3w_2 & v_3w_3 \end{pmatrix}\]](https://www.weiy.city/wp-content/ql-cache/quicklatex.com-82e047f61ecdefcc15da3fa3e3a1f86f_l3.png)
![]()
![]() is called tensor product of
is called tensor product of ![]() and
and ![]() .
.


