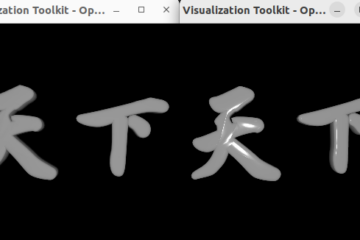
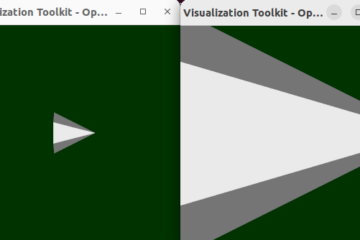
The Geometry Meaning Of The Determinant

The geometry meaning of the determinant is the sign volumn value for three vectors in 3D world or a sign area value of two vectors (parallelogram) in the 2D coordinate system.

For three points in the 2D world:

The triangle is counterclockwise ordered if and clockwise ordered if . If , these points are collinear.

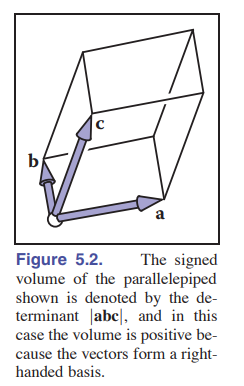
For three vectors in the 3D world, It’s sign volumn value for three vectors.

#include "point.hpp"

#include <vtkSmartPointer.h>
#include <vtkPolyData.h>
#include <vtkMatrix3x3.h>
#include <vtkMath.h>

using namespace std;

int main()
{
    Point pt0( 0, 0, 0 );
    Point pt1( 0, 1, 0 );
    Point pt2( 1, 1, 0 );
    // three points are on the same plane

    vtkSmartPointer<vtkMatrix3x3> matrix = vtkSmartPointer<vtkMatrix3x3>::New();
    double value[3][3] = { { 1, 1, 1 }, { pt0[0], pt1[0], pt2[0] }, { pt0[1], pt1[1], pt2[1] } };
    for( int i = 0; i < 3; ++i ){
        for( int j = 0; j < 3; ++j ){
            matrix->SetElement( i, j, value[i][j] );
        }
    }
    std::cout << "det: " << matrix->Determinant() << std::endl; // det: -1 ; means they are clockwise

    pt2 = Point( 0, -1, 0 );
    matrix->SetElement( 1, 2, pt2[0] );
    matrix->SetElement( 2, 2, pt2[1] );
    std::cout << "det: " << matrix->Determinant() << std::endl; // det: 0 ; means three vertices are collinear

    // three vectors in the 3D world
    pt0 = Point( 0, 0, 1 );
    pt1 = Point( 0, 1, 1 );
    pt2 = Point( -1, 1, -1 );

    std::cout << "det: " << vtkMath::Determinant3x3( pt0.point, pt1.point, pt2.point ) << std::endl; // det: 1; means three vertices are counterclockwise
    return 0;
}