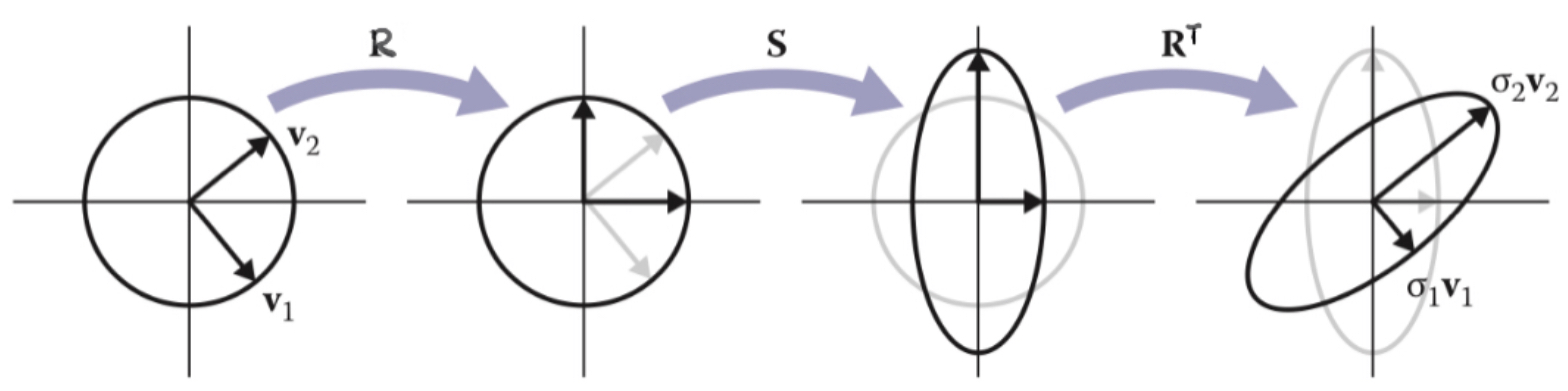
The Matrix Of Rotate Around The Axis In 3d

As with 2D transforms, any 3D transformation matrix can be decomposed using SVD into a rotation, scale, and another rotation.
Any symmetric 3D matrix has an eigenvalue decomposition into rotation, scale, and inverse-rotation.
Finally, a 3D rotation can be decomposed into a product of 3D shear matrices.

Rotate about z-axis:

$rotateZ(\phi) = \begin{pmatrix} cos\phi & -sin\phi & 0 \\ sin\phi & cos\phi & 0 \\ 0 & 0 & 1 \end{pmatrix}$

Rotate about x-axis:

$rotateX(\phi) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & cos\phi & -sin\phi \\ 0 & sin\phi & cos\phi \end{pmatrix}$

Rotate about y-axis:

$rotateY(\phi) = \begin{pmatrix} cos\phi & 0 & sin\phi \\ 0 & 1 & 0 \\ -sin\phi & 0 & cos\phi \end{pmatrix}$

The inverse of an orthogonal matrix is awalys its transpose.
So if there is a rotate matrice $R_{uvw}$ of 3D object, $R_{uvw}^T = R_{uvw}^{-1}$ .

For example,

$rotateZ(\phi)^{T} = \begin{pmatrix} cos\phi & sin\phi & 0 \\ -sin\phi & cos\phi & 0 \\ 0 & 0 & 1 \end{pmatrix}$

Then we have:

$rotateZ(\phi) \times rotateZ(\phi)^{T} = E$

So we get:

$rotateZ(\phi)^{T} = rotateZ(\phi)^{-1}$

Here is a way to scale object along the direction (1, 1, 0). Rotate the vector(1, 1, 0) to the standard asix firstly, scale it along Y axis and rotate it back finally.
The whole process can be written $RSR^T$ .
$R^T$ is equivalent to $R^{-1}$ in this scene.