The Relationship Between 3D Coordinate Value XYZ And 2D Texture Coordinate UVR – weiy.city

We will introduce the transformation equation for 3D Coordinate Value XYZ And 2D Texture Coordinate UVR.
Try to represent the UVR value by x,y, and z.
Here is derivation process.

$[x, y, z] = [ r\cos(p) \cos(h) , r \cos(p) \sin(h), r \sin(p) ]$

$\frac{y}{x} = \frac{\sin(h)}{\cos(h)} = \tan(h)$

$\longrightarrow h=\arctan(\frac{y}{x})$

$x^2+y^2=r^2\cos^2(p)\cos^2(h) + r^2\cos^2(p)\sin^2(h)=r^2\cos^2(p)$

$z^2=r^2\sin^2(p)$

$x^2+y^2+z^2=r^2$

$\longrightarrow r = \sqrt{x^2+y^2+z^2}$

$\sin(p) = \frac{z}{r}$

$\longrightarrow p = \arcsin(\frac{z}{r})$

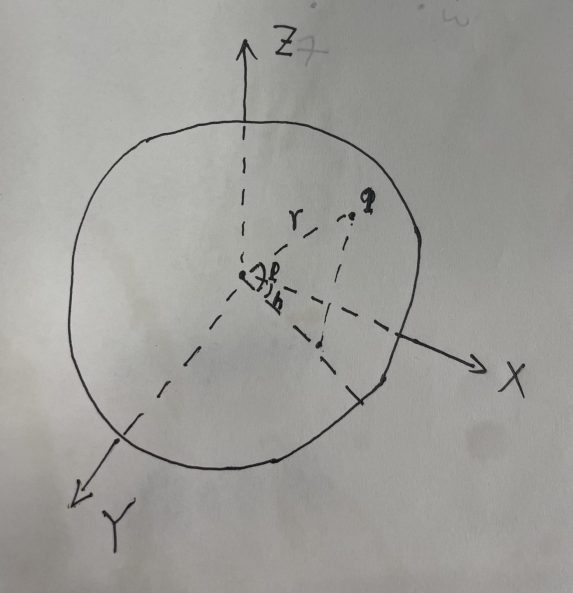
Because U and V are radians, so we have

$u = \arctan(\frac{y}{x}) / PI \qquad \longleftarrow h$

$v = \arcsin(\frac{z}{r}) / PI \qquad \longleftarrow p$

$r = \sqrt{x^2+y^2+z^2}$

Categories: Math

Tags: math

0 0 votes

Article Rating

Subscribe

0 Comments

Inline Feedbacks

View all comments

Tex To PDF
: convert the Latex file which suffix is tex to a PDF file

Got it!

X

0

Would love your thoughts, please comment.x

()