Angles Returns By vtkTransform::GetOrientation

The interface vtkTransform::GetOrientation returns Euler angles to describes the orientation of a rigid body.
The order of rotation axes in this process is Z, X, Y, but the solving sequence in the interface code is reversed.
The implementation details about the interface are here. (from VTK8.2.0)

//----------------------------------------------------------------------------
// Get the x, y, z orientation angles from the transformation matrix as an
// array of three floating point values.
void vtkTransform::GetOrientation(double orientation[3],
                                  vtkMatrix4x4 *amatrix)
{
#define VTK_AXIS_EPSILON 0.001
#define VTK_ORTHO_EPSILON 4e-16
  int i;

  // convenient access to matrix
  double (*matrix)[4] = amatrix->Element;
  double ortho[3][3];

  for (i = 0; i < 3; i++)
  {
    ortho[0][i] = matrix[0][i];
    ortho[1][i] = matrix[1][i];
    ortho[2][i] = matrix[2][i];
  }
  if (vtkMath::Determinant3x3(ortho) < 0)
  {
    ortho[0][2] = -ortho[0][2];
    ortho[1][2] = -ortho[1][2];
    ortho[2][2] = -ortho[2][2];
  }

  // Check whether matrix is orthogonal
  double r1 = vtkMath::Dot(ortho[0],ortho[1]);
  double r2 = vtkMath::Dot(ortho[0],ortho[2]);
  double r3 = vtkMath::Dot(ortho[1],ortho[2]);

  // Orthogonalize the matrix if it isn't already orthogonal
  if ((r1*r1) + (r2*r2) + (r3*r3) > (VTK_ORTHO_EPSILON*VTK_ORTHO_EPSILON))
  {
    vtkMath::Orthogonalize3x3(ortho, ortho);
  }

  // compute the max scale as we need that for the epsilon test
  double scale0 = vtkMath::Norm(ortho[0]);
  double scale1 = vtkMath::Norm(ortho[1]);
  double maxScale = vtkMath::Norm(ortho[2]);
  maxScale = maxScale >= scale0 ? maxScale : scale0;
  maxScale = maxScale >= scale1 ? maxScale : scale1;
  if (maxScale == 0.0)
  {
    orientation[0] = 0.0;
    orientation[1] = 0.0;
    orientation[2] = 0.0;
    return;
  }

  // first rotate about y axis
  double x2 = ortho[2][0];
  double y2 = ortho[2][1];
  double z2 = ortho[2][2];

  double x3 = ortho[1][0];
  double y3 = ortho[1][1];
  double z3 = ortho[1][2];

  double d1 = sqrt(x2*x2 + z2*z2);

  double cosTheta, sinTheta;
  if (d1 < VTK_AXIS_EPSILON*maxScale)
  {
    cosTheta = 1.0;
    sinTheta = 0.0;
  }
  else
  {
    cosTheta = z2/d1;
    sinTheta = x2/d1;
  }

  double theta = atan2(sinTheta, cosTheta);
  orientation[1] = - vtkMath::DegreesFromRadians( theta );

  // now rotate about x axis
  double d = sqrt(x2*x2 + y2*y2 + z2*z2);

  double sinPhi, cosPhi;
  if (d < VTK_AXIS_EPSILON * maxScale)
  {
    sinPhi = 0.0;
    cosPhi = 1.0;
  }
  else if (d1 < VTK_AXIS_EPSILON * maxScale)
  {
    sinPhi = y2/d;
    cosPhi = z2/d;
  }
  else
  {
    sinPhi = y2/d;
    cosPhi = (x2*x2 + z2*z2)/(d1*d);
  }

  double phi = atan2(sinPhi, cosPhi);
  orientation[0] = vtkMath::DegreesFromRadians( phi );

  // finally, rotate about z
  double x3p = x3*cosTheta - z3*sinTheta;
  double y3p = - sinPhi*sinTheta*x3 + cosPhi*y3 - sinPhi*cosTheta*z3;
  double d2 = sqrt(x3p*x3p + y3p*y3p);

  double cosAlpha, sinAlpha;
  if (d2 < VTK_AXIS_EPSILON * maxScale)
  {
    cosAlpha = 1.0;
    sinAlpha = 0.0;
  }
  else
  {
    cosAlpha = y3p/d2;
    sinAlpha = x3p/d2;
  }

  double alpha = atan2(sinAlpha, cosAlpha);
  orientation[2] = vtkMath::DegreesFromRadians( alpha );
}

We can write a test program to use Euler angles fto re-generate model’s rotation matrix.
Let’s rotate a cone around Y axes about 30 degrees and rotate a cone around Z 30 degrees.
Analyze the matrix and get it’s orientation, then use Euler angles to forms a new rotate matrix. Compare the new matrix and old matrix, they represent same result.

#include <iostream>
#include <vtkSmartPointer.h>
#include <vtkSphereSource.h>
#include <vtkActor.h>
#include <vtkConeSource.h>
#include <vtkRenderer.h>
#include <vtkRenderWindow.h>
#include <vtkPolyDataMapper.h>
#include <vtkRenderWindowInteractor.h>
#include <vtkAxesActor.h>
#include <vtkTransform.h>
#include <vtkPlane.h>

#include "point.hpp"

#define vtkSPtr vtkSmartPointer
#define vtkSPtrNew(Var, Type) vtkSPtr<Type> Var = vtkSPtr<Type>::New();

using namespace std;

int main()
{
    vtkSPtrNew( cone, vtkConeSource );
    vtkSPtrNew( mapper, vtkPolyDataMapper );
    mapper->SetInputConnection( cone->GetOutputPort() );

    vtkSPtrNew( actor, vtkActor );
    actor->SetMapper( mapper );

    vtkSPtrNew( trans, vtkTransform );
    trans->RotateY( 30 );
    trans->RotateZ( 30 );
    trans->Update();

    trans->GetMatrix()->PrintSelf( std::cout, vtkIndent() );

    actor->SetUserTransform( trans );

    double oritentation[3];
    double wxyz[4];
    trans->GetOrientation( oritentation );
    trans->GetOrientationWXYZ( wxyz );
    std::cout << "oritentation: " << oritentation[0] << ", " << oritentation[1] << ", " << oritentation[2] << std::endl;
    std::cout << "wxyz: " << wxyz[0] << ", " << wxyz[1] << ", " << wxyz[2] << ", " << wxyz[3] << std::endl;

    vtkSPtrNew( testTrans, vtkTransform );
    testTrans->RotateZ( oritentation[2] );
    testTrans->RotateX( oritentation[0] );
    testTrans->RotateY( oritentation[1] );
    testTrans->Update();
    testTrans->GetMatrix()->PrintSelf( std::cout, vtkIndent() );

    vtkSPtrNew( testTrans1, vtkTransform );
    testTrans1->RotateWXYZ( wxyz[0], wxyz[1], wxyz[2], wxyz[3] );
    testTrans1->Update();
    testTrans1->GetMatrix()->PrintSelf( std::cout, vtkIndent() );

    vtkSPtrNew( renderer, vtkRenderer );
    renderer->AddActor(actor);
    renderer->SetBackground( 0, 0, 0 );

    vtkSPtrNew( renderWindow, vtkRenderWindow );
    renderWindow->AddRenderer( renderer );

    vtkSPtrNew( renderWindowInteractor, vtkRenderWindowInteractor );
    renderWindowInteractor->SetRenderWindow( renderWindow );

    vtkSPtrNew( axes, vtkAxesActor );
    renderer->AddActor( axes );

    renderer->ResetCamera();
    renderWindow->Render();
    renderWindowInteractor->Start();
    return 0;
}

Output:

Debug: Off
Modified Time: 114
Reference Count: 1
Registered Events: (none)
Elements:
0.75 -0.433013 0.5 0 
0.5 0.866025 0 0 
-0.433013 0.25 0.866025 0 
0 0 0 1 

oritentation: 14.4775, 26.5651, 26.5651

wxyz: 42.1812, 0.186157, 0.694747, 0.694747

Debug: Off
Modified Time: 133
Reference Count: 1
Registered Events: (none)
Elements:
0.75 -0.433013 0.5 0 
0.5 0.866025 0 0 
-0.433013 0.25 0.866025 0 
0 0 0 1 

Debug: Off
Modified Time: 144
Reference Count: 1
Registered Events: (none)
Elements:
0.75 -0.433013 0.5 0 
0.5 0.866025 0 0 
-0.433013 0.25 0.866025 0 
0 0 0 1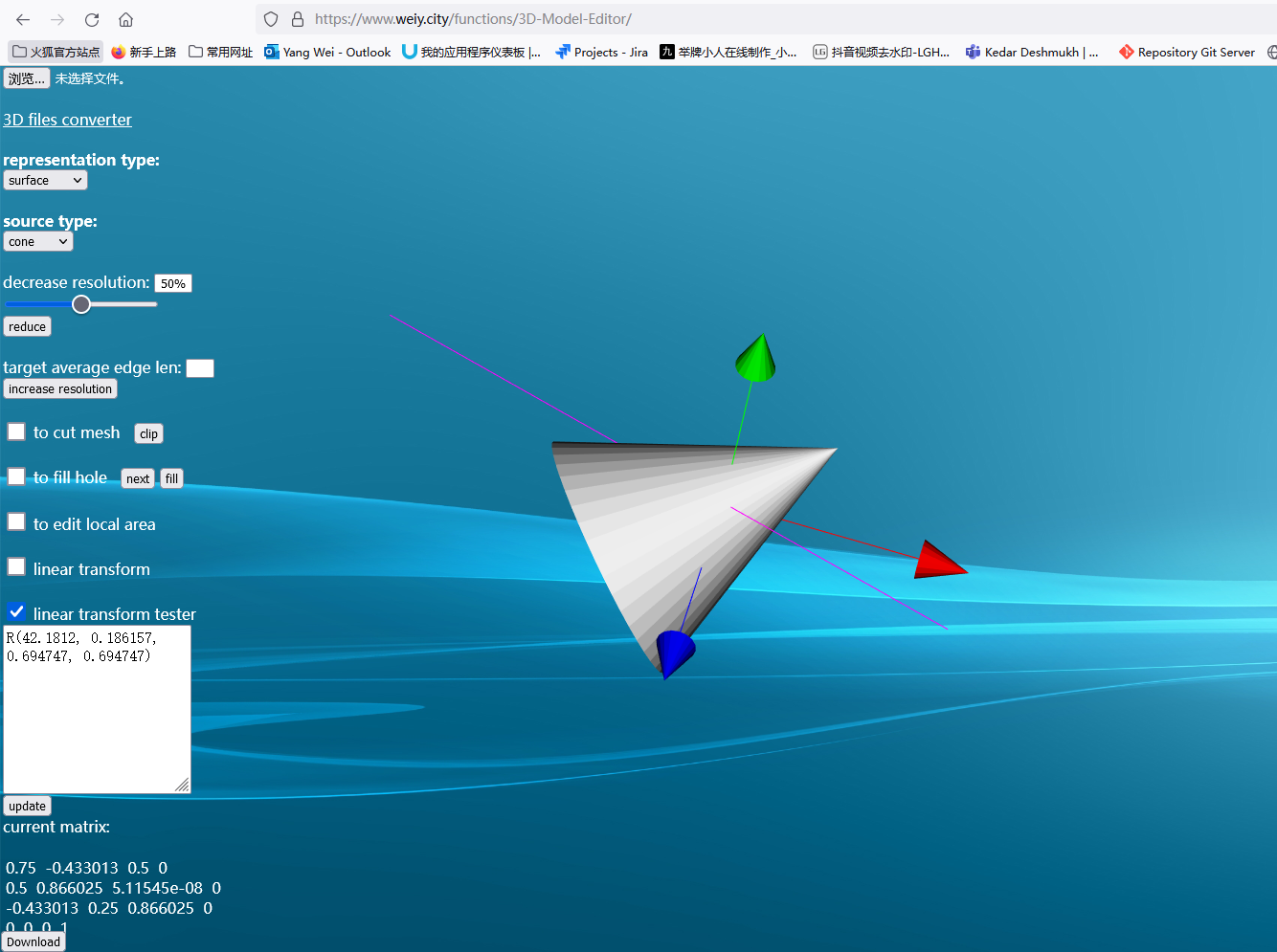 

So we can find that the wxyz (quaternion) matrix, Euler angles matrix, and original rotating matrix have same elements.
You also test the process in our online tool 3D Model Editor‘s linear transform tester function.